leetcode-动态规划题型
动态规划是一种解决问题的算法策略,它通常用于解决涉及最优化问题的情况,比如找到最短路径、最大价值等等。动态规划算法的核心思想是将一个大问题分解成一系列小问题,并记住已经解决的小问题的答案,以避免重复计算。这种方法有助于提高计算效率。
动态规划的一般步骤如下:
- 定义问题: 首先,将大问题分解成小问题,并明确定义每个小问题的状态。这些状态是问题的不同方面,通常与问题的输入相关。
- 找到递推关系: 接下来,确定每个状态如何与其他状态相关联。这通常通过递推关系或方程式来完成,它们描述了一个状态如何由一个或多个先前状态计算得出。
- 初始化: 对于问题中的一些状态,需要初始化其初始值,以便递推关系可以开始工作。
- 计算和记忆: 使用递推关系,从最小的状态开始,逐步计算并记住每个状态的值。这些值可以保存在表格、数组或字典中,以便后续使用。
- 解决大问题: 通过计算小问题的值,最终可以解决整个大问题。这通常是在表格中找到最终状态的值,然后根据需要提取答案。
- 优化: 可能需要进一步优化算法以减少内存和时间的消耗。
买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
股票问题的方法就是 动态规划,因为它包含了重叠子问题,即买卖股票的最佳时机是由之前买或不买的状态决定的,而之前买或不买又由更早的状态决定的…
由于本题只有一笔交易(买入卖出),因此除了动态规划,我们还可以使用更加简便的方法实现。
遍历一遍数组,计算每次 到当天为止 的最小股票价格和最大利润。
1 | int maxProfit(vector<int>& prices) { |
买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
遍历整个股票交易日价格列表 price,策略是所有上涨交易日都买卖(赚到所有利润),所有下降交易日都不买卖(永不亏钱)。
- 设 tmp 为第 i-1 日买入与第 i 日卖出赚取的利润,即 tmp = prices[i] - prices[i - 1] ;
- 当该天利润为正 tmp > 0,则将利润加入总利润 profit;当利润为 0 或为负,则直接跳过;
- 遍历完成后,返回总利润 profit。
1 | int maxProfit(vector<int>& prices) { |
最大正方形
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
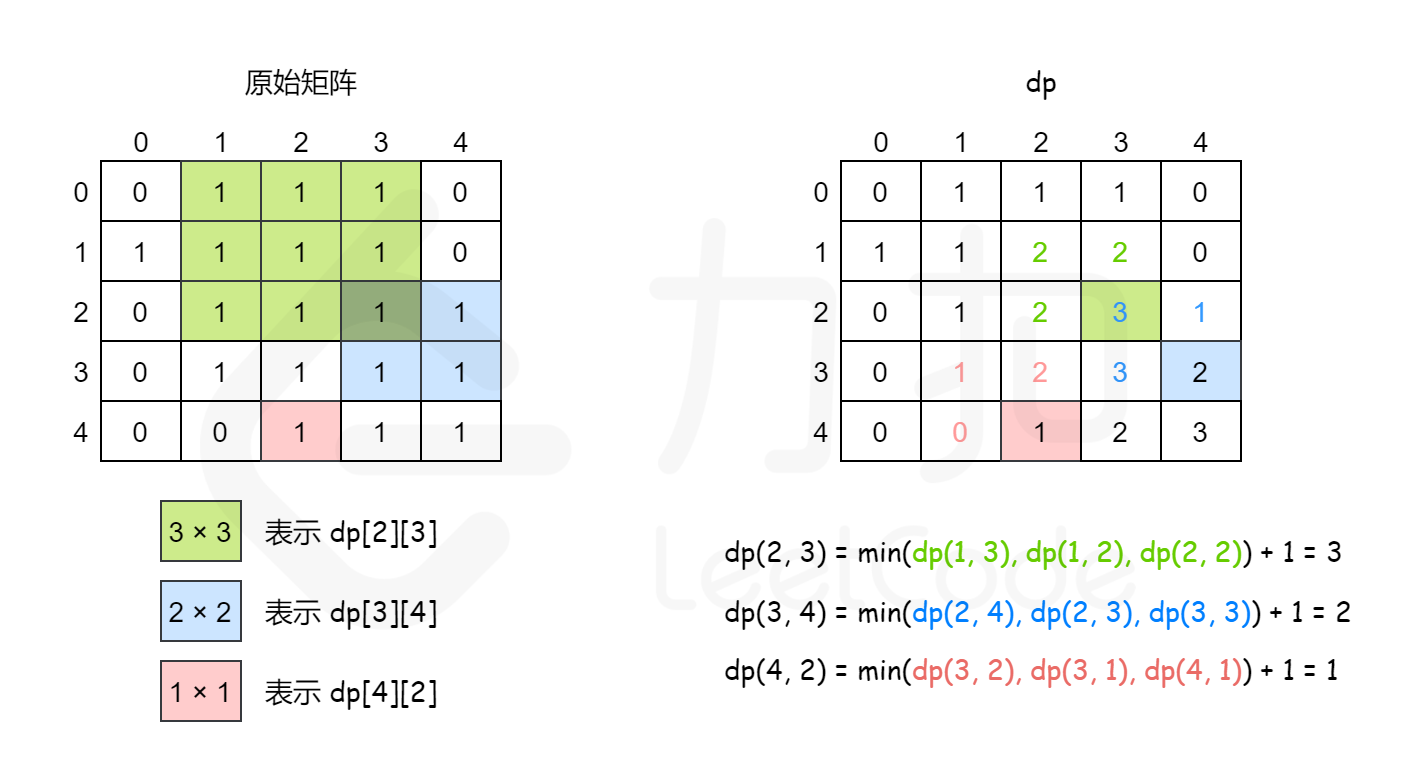
dp(i,j)=min(dp(i-1,j),dp(i-1,j-1),dp(i,j-1)) + 1
以下用一个例子具体说明。原始矩阵如下。
0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1
对应的 dp值如下。
0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3
此外,还需要考虑边界条件。如果 i 和 j 中至少有一个为 0,则以位置 (i,j) 为右下角的最大正方形的边长只能是1,因此dp(i,j)=1。
1 | int maximalSquare(vector<vector<char>>& matrix) { |
最长有效括号
给你一个只包含 ‘(‘ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
首先,我们定义一个dp 数组,其中第 i 个元素表示以下标为 i 的字符结尾的最长有效子字符串的长度。
对于最优的策略,一定有最后一个元素 s[i].
所以,我们先看第 i 个位置,这个位置的元素 s[i]可能有如下两种情况:
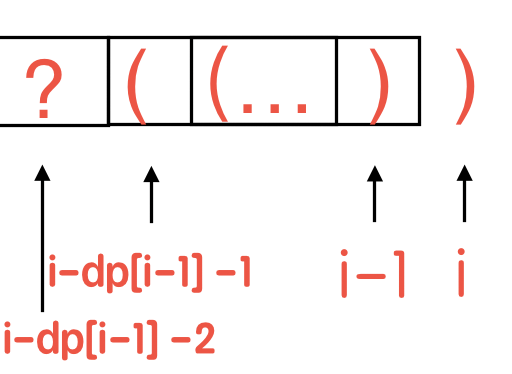
1 | if s[i] == '(' : |
最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
定义状态(定义子问题)
dp[i]:表示以 nums[i] 结尾 的 连续 子数组的最大和。
假设数组 nums 的值全都严格大于 0,那么一定有 dp[i] = dp[i - 1] + nums[i]。
可是 dp[i - 1] 有可能是负数,于是分类讨论:
- 如果 dp[i - 1] > 0,那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面,得到和更大的连续子数组;
- 如果 dp[i - 1] <= 0,那么 nums[i] 加上前面的数 dp[i - 1] 以后值不会变大。于是 dp[i] 「另起炉灶」,此时单独的一个 nums[i] 的值,就是 dp[i]。
dp[i]=max{nums[i],dp[i−1]+nums[i]}
dp[0] 根据定义,只有 1 个数,一定以 nums[0] 结尾,因此 dp[0] = nums[0]。
根据「状态转移方程」,dp[i] 的值只和 dp[i - 1] 有关,因此可以使用「滚动变量」的方式将代码进行优化。
为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做「无后效性」。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍历就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的「状态」,图中的边则对应状态之间的「转移」,转移的选取就是动态规划中的「决策」。
解决「有后效性」的办法是固定住需要分类讨论的地方,记录下更多的结果。在代码层面上表现为:
- 状态数组增加维度,例如:「力扣」的股票系列问题;
- 把状态定义得更细致、准确,例如:前天推送的第 124 题:状态定义只解决路径来自左右子树的其中一个子树。
1 | public class Solution { |