队列
循环队列,固定容器大小,实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include <iostream>
using namespace std;
const int MAX_QUEUE_SIZE = 102;
template<typename T>
class Node {
public:
T data;
Node<T>* next;
};
template<typename T>
class CircularQueue {
public:
CircularQueue(): front(NULL), rear(NULL), size(0) {}
bool enqueue(T data);
bool dequeue(T& data);
bool isFull() { return size == MAX_QUEUE_SIZE; }
bool isEmpty() { return size == 0; }
int getSize() { return size; }
void printQueue();
private:
Node<T>* front;
Node<T>* rear;
int size;
};
template<typename T>
bool CircularQueue<T>::enqueue(T data) {
if (isFull()) {
if (front == NULL) {
return false;
}
front->data = data;
front = front->next;
rear = rear->next;
} else {
Node<T>* newNode = new Node<T>();
newNode->data = data;
newNode->next = front;
if (isEmpty()) {
front = newNode;
rear = newNode;
} else {
rear->next = newNode;
rear = newNode;
}
size++;
}
return true;
}
template<typename T>
bool CircularQueue<T>::dequeue(T& data) {
if (isEmpty()) {
return false;
}
Node<T>* temp = front;
data = temp->data;
front = front->next;
delete temp;
size--;
return true;
}
template<typename T>
void CircularQueue<T>::printQueue() {
if (isEmpty()) {
cout << "Queue is empty" << endl;
} else {
Node<T>* temp = front;
while (temp != rear) {
cout << temp->data << " ";
temp = temp->next;
}
cout << rear->data << " " << endl;
}
}
int main() {
CircularQueue<int> q;
for (int i = 0; i < 100; i++) {
q.enqueue(i);
}
q.printQueue();
q.enqueue(100);
q.enqueue(101);
q.enqueue(102);
q.enqueue(103);
q.enqueue(104);
q.printQueue();
return 0;
}
|
在用数组实现的非循环队列中,队满的判断条件是 tail == n,队空的判断条件是 head == tail。那针对循环队列,如何判断队空和队满呢?
队列为空的判断条件仍然是 head == tail。但队列满的判断条件就稍微有点复杂了。
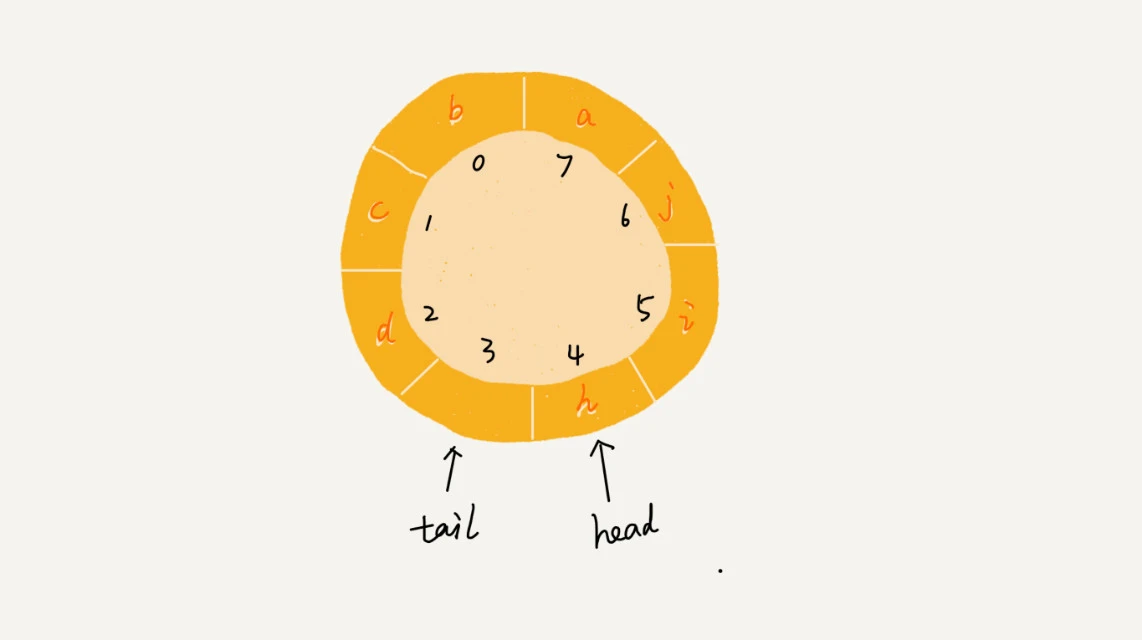
就像我图中画的队满的情况,tail=3,head=4,n=8,所以总结一下规律就是:(3+1)%8=4。多画几张队满的图,你就会发现,当队满时,(tail+1)%n=head。
你有没有发现,当队列满时,图中的 tail 指向的位置实际上是没有存储数据的。所以,循环队列会浪费一个数组的存储空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public class CircularQueue {
private String[] items;
private int n = 0;
private int head = 0;
private int tail = 0;
public CircularQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
public boolean enqueue(String item) {
if ((tail + 1) % n == head) return false;
items[tail] = item;
tail = (tail + 1) % n;
return true;
}
public String dequeue() {
if (head == tail) return null;
String ret = items[head];
head = (head + 1) % n;
return ret;
}
}
|
基于链表的实现方式,可以实现一个支持无限排队的无界队列(unbounded queue),但是可能会导致过多的请求排队等待,请求处理的响应时间过长。所以,针对响应时间比较敏感的系统,基于链表实现的无限排队的线程池是不合适的。
而基于数组实现的有界队列(bounded queue),队列的大小有限,所以线程池中排队的请求超过队列大小时,接下来的请求就会被拒绝,这种方式对响应时间敏感的系统来说,就相对更加合理。不过,设置一个合理的队列大小,也是非常有讲究的。队列太大导致等待的请求太多,队列太小会导致无法充分利用系统资源、发挥最大性能。
实际上,对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。
简述堆
- 堆是一种完全二叉树形式,其可分为最大值堆和最小值堆。
- 最大值堆:子节点均小于父节点,根节点是树中最大的节点。
- 最小值堆:子节点均大于父节点,根节点是树中最小的节点。
简述满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
简述希尔排序
希尔排序:把记录按下标的一定增量分组,对每组进行直接插入排序,每次排序后减小增量,当增量减至 1 时排序完毕。
排序算法不稳定。时间复杂度 O(nlogn),空间复杂度 O(1)。
常见的不稳定排序算法有哪些
希尔排序、直接选择排序、堆排序、快速排序
常见的稳定排序算法有哪些
插入排序、冒泡排序、归并排序
简述红黑树
红黑树本身是有2-3树发展而来,红黑树是保持黑平衡的二叉树,其查找会比AVL树慢一点,添加和删除元素会比AVL树快一点。增删改查统计性能上讲,红黑树更优。 红黑树主要特征是在每个节点上增加一个属性表示节点颜色,可以红色或黑色。红黑树和 AVL 树类似,都是在进行插入和删除时通过旋转保持自身平衡,从而获得较高的查找性能。红黑树保证从根节点到叶尾的最长路径不超过最短路径的 2 倍,所以最差时间复杂度是 O(logn)。红黑树通过重新着色和左右旋转,更加高效地完成了插入和删除之后的自平衡调整。
二叉搜索树和平衡二叉树有什么关系,强平衡二叉树(AVL树)和弱平衡二叉树(红黑树)有什么区别,及其代表数据结构?
二叉搜索树也叫二叉查找树、二叉排序树。要么是一颗空树,要么就是需要具有一些性质:
任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点。
平衡二叉树是在二叉搜索树的基础上多了两个重要的特点:
(1)左右两子树的高度差的绝对值不能超过 1;
(2)左右两子树也是一颗平衡二叉树。
红黑树是在普通二叉树的基础上,对每个节点添加一个颜色属性形成的,需要同时满足五条性质:
(1)节点是红色或者是黑色;
(2)根节点是黑色;
(3)每个叶子节点(NIL 或空节点)是黑色;
(4)每个红色节点的两个子节点都是黑色的(也就是说不存在两个连续的红色节点);
(5)从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
AVL 树需要保持平衡,但它的旋转太耗时,红黑树就是一个没有 AVL 树那样平衡,因此插入、删除效率会高于 AVL 树,而 AVL树的查找效率高于红黑树。
